Question

What is the solution to the equation below?

Answer 1

Answer: Option C.

Explanation:

First, we need to square both sides of the equation:

`√(x+3)=x-3\\\\(√(x+3))^2=(x-3)^2`

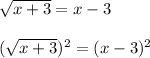
We know that:

`(a-b)^2=a^2-2ab+b^2`

Then, applying this, we get:

`x+3=x^2-2(x)(3)+3^2\\\\x+3=x^2-6x+9`

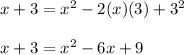
Now we need to subtract "x" and 3 from both sides of the equation:

`x+3-(x)-(3)=x^2-6x+9-(x)-(3)\\\\0=x^2-6x+9-x-3`

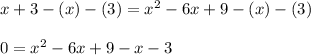
Adding like terms:

`0=x^2-7x+6`

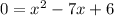
Factor the quadratic equation. Find two numbers whose sum be -7 and whose product be 6. These numbers are: -1 and -6. Then:

`(x-1)(x-6)=0`

Then:

`x_1=1\\x_2=6`

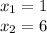
Checking the first solution is correct:

`√(1+3)=1-3\\ 2=-2 \ (False)`

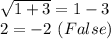
Checking the second solution is correct:

`√(6+3)=6-3\\ 3=3 \ (True)`

Answer 2

C x=6

Explanation:

sqrt(x+3) = x-3

Square each side

(sqrt(x+3))^2 = (x-3)^2

x+3 = (x-3)^2

x+3 = (x-3)(x-3)

FOIL

x+3 = x^2 -3x-3x+9

Combine like terms

x+3 = x^2 -6x+9

Subtract x from each side

x-x+3 = x^2 -6x-x +9

3 = x^2 -7x +9

Subtract 3 from each side

3-3 = x^2 -7x +9-3

0 = x^2 -7x+6

Factor

0 = (x-6)(x-1)

Using the zero product property

x-6=0 x-1 =0

x=6 x=1

Since we squared we need to check for extraneous solutions

x=1

sqrt(1+3) = 1-3

sqrt(4) = -2

2=-2

False

Extraneous

x=6

sqrt(6+3) = 6-3

sqrt(9) = 3

3=3

True solutions