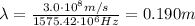Question

CP Global Positioning System (GPS). The GPS network consists of 24 satellites, each of which makes two orbits around the earth per day. Each satellite transmits a 50.0-W (or even less) sinusoidal electromagnetic signal at two frequencies, one of which is 1575.42 MHz. Assume that a satellite transmits half of its power at each frequency and that the waves travel uni- formly in a downward hemisphere. (a) What average intensity does a GPS receiver on the ground, directly below the satellite, receive? (Hint: First use Newton’s laws to find the altitude of the satellite.) (b) What are the amplitudes of the electric and magnetic fields at the GPS receiver in part (a), and how long does it take the signal to reach the receiver? (c) If the receiver is a square panel 1.50 cm on a side that absorbs all of the beam, what average pres- sure does the signal exert on it? (d) What wavelength must the receiver be tuned to?

Answer 1

(a)
`9.66\cdot 10^(-15) W/m^2`

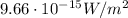
First of all, we need to find the altitude of the satellite. The gravitational attraction between the Earth and the satellite is equal to the centripetal force that keeps the satellite in circular motion, so

`G(mM)/(r^2)=m\omega^2 r` (1)

where

G is the gravitational constant

m is the satellite's mass

M is the earth's mass

r is the distance of the satellite from the Earth's centre

`\omega` is the angular frequency of the satellite

The satellite here makes two orbits around the Earth per day, so its frequency is

`\omega = \frac {2 (rev)/(day)}{24 (h)/(day) \cdot 60 (min)/(h)} \cdot (2\pi rad/rev)/(s/min)=1.45\cdot 10^(-4) rad/s`

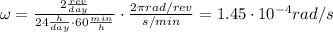
And by solving eq.(1) for r, we find

`r=\sqrt[3]{(GM)/(\omega^2)}=\sqrt[3]{((6.67\cdot 10^(-11))(5.98\cdot 10^(24)kg))/((1.45\cdot 10^(-4) rad/s)^2)}=2.67\cdot 10^(7) m`

The radius of the Earth is

`R=6.37\cdot 10^6 m`

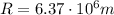
So the altitude of the satellite is

`h=r-R=2.67\cdot 10^7 m-6.37\cdot 10^6m=2.03\cdot 10^7 m`

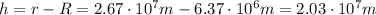
The average intensity received by a GPS receiver on the Earth will be given by

`I=(P)/(A)`

where

P = 50.0 W is the power

A is the area of a hemisphere, which is:

`A=4\pi h^2 = 4 \pi (2.03\cdot 10^7 m)^2=5.18\cdot 10^(15) m^2`

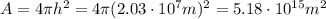
So the intensity is

`I=(50.0 W)/(5.18\cdot 10^(15)m^2)=9.66\cdot 10^(-15) W/m^2`

(b)
`2.70\cdot 10^(-6) V/m, 9.0\cdot 10^(-15)T`, 0.068 s

The relationship between average intensity of an electromagnetic wave and amplitude of the electric field is

`I=(1)/(2)c\epsilon_0 E^2`

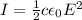
where

c is the speed of light

`\epsilon_0` is the vacuum permittivity

E is the amplitude of the electric field

Solving for E, we find

`E=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(9.66\cdot 10^(-15) W/m^2))/((3\cdot 10^8 m/s)(8.85\cdot 10^(-12)F/m))}=2.70\cdot 10^(-6) V/m`

Instead, the amplitude of the magnetic field is given by:

`B=(E)/(c)=(2.70\cdot 10^(-6) V/m)/(3\cdot 10^8 m/s)=9.0\cdot 10^(-15)T`

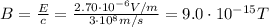
The signal travels at the speed of light, so the time it takes to reach the Earth is the distance covered divided by the speed of light:

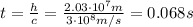
`t=(h)/(c)=(2.03\cdot 10^7 m)/(3\cdot 10^8 m/s)=0.068 s`

(c)
`3.22\cdot 10^(-23)Pa`

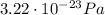
In case of a perfect absorber (as in this case), the radiation pressure exerted by an electromagnetic wave on a surface is given by

`p=(I)/(c)`

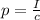
where

I is the average intensity

c is the speed of light

In this case, we have

`I=9.66\cdot 10^(-15) W/m^2`

So the average pressure is

`p=(9.66\cdot 10^(-15) W/m^2)/(3\cdot 10^8 m/s)=3.22\cdot 10^(-23)Pa`

(d) 0.190 m

The wavelength of the receiver must be tuned to the same wavelength as the transmitter (the satellite), which is given by

`\lambda=(c)/(f)`

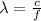
where

c is the speed of light

f is the frequency of the signal

For the satellite in the problem, the frequency is

`f=1575.42 MHz=1575.42\cdot 10^6 Hz`

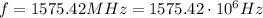
So the wavelength of the signal is:

`\lambda=(3.0\cdot 10^8 m/s)/(1575.42 \cdot 10^6 Hz)=0.190 m`