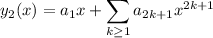Question

Use power series to find two linearly independent solutions of y''-2xy'+4y = 0

Answer 1

Assume a general solution of the form

`y(x)=\displaystyle\sum_(n\ge0)a_nx^n`

with derivatives

`y'(x)=\displaystyle\sum_(n\ge0)na_nx^(n-1)=\sum_(n\ge1)na_nx^(n-1)`

`y''(x)=\displaystyle\sum_(n\ge0)n(n-1)a_nx^(n-2)=\sum_(n\ge2)n(n-1)a_nx^(n-2)`

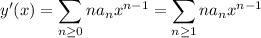
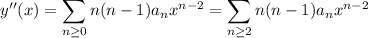
Substituting into the ODE gives

`\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)-2\sum_(n\ge1)na_nx^n+4\sum_(n\ge0)a_nx^n=0`

The first sum starts with degree 0; the second starts with degree 1; and the third starts with degree 0. So remove the first term from the first and third sums, then consolidate everything into one sum by shifting indices as needed.

First sum:

`\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)=2a_2+\sum_(n\ge3)n(n-1)a_nx^(n-2)`

`\displaystyle\sum_(n\ge2)n(n-1)a_nx^(n-2)=2a_2+\sum_(n\ge1)(n+2)(n+1)a_(n+2)x^n`

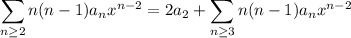
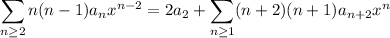
Third sum:

`\displaystyle\sum_(n\ge0)a_nx^n=a_0+\sum_(n\ge1)a_nx^n`

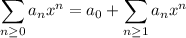
So the ODE can be expressed as

`\displaystyle\left(2a_2+\sum_(n\ge1)(n+2)(n+1)a_(n+2)x^n\right)-2\sum_(n\ge1)na_nx^n+4\left(a_0+\sum_(n\ge1)a_nx^n\right)=0`

`\displaystyle2a_2+4a_0+\sum_(n\ge1)\bigg((n+2)(n+1)a_(n+2)+(4-2n)a_n\bigg)x^n=0`

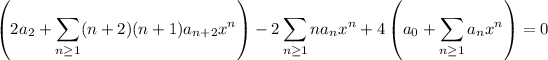
Then the coefficients are given by the recurrence,

`\begin{cases}a_0=a_0\\a_1=a_1\\2(2-n)a_n+(n+2)(n+1)a_(n+2)=0&\text{for }n\ge0\end{cases}`

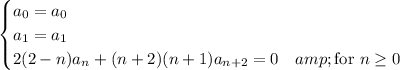
Notice that we should have
`a_0\\eq0` and
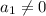`a_1\\eq0` in order to get non-zero solutions.

For
`n=2`, we would find that
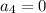`a_4=0`, which would imply that
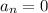`a_n=0` for all even
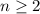`n\ge2`. Then the even-indexed terms in the series contribute one solution,

`y_1(x)=a_0+a_2x^2=a_0(1-2x^2)`.

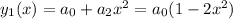On the other hand, for odd
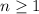`n\ge1` we have

`a_(n+2)=(2(n-2))/((n+2)(n+1))a_n`

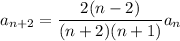
With
`n=1`:

`a_3=(2\cdot(-1))/(3\cdot2)a_1=-\frac2{3!}a_1`

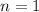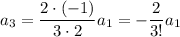
With
`n=3`:

`a_5=(2\cdot1)/(5\cdot4)a_3=-(2^2\cdot1)/(5!)a_1`

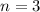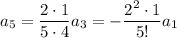
With
`n=5`:

`a_7=(2\cdot3)/(7\cdot6)a_5=-(2^3\cdot3\cdot1)/(7!)a_1`

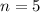So the general pattern for
`n=2k+1`,
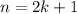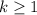`k\ge1`, is

`a_(2k+1)=-(2^k\prod\limits_(i=1)^(k-1)(2i-1))/((2k+1)!)a_1`

and we get a second (linearly independent) solution

`y_2(x)=a_1x+\displaystyle\sum_(k\ge1)a_(2k+1)x^(2k+1)`