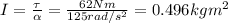Question

The triceps muscle in the back of the upper arm extends the forearm. This muscle in a professional boxer exerts a force of 2.00 X 10^3 N with an effective perpendicular lever arm of 3.10 cm, producing an angular acceleration of the forearm of 125 rad/s2. What is the moment of inertia of the boxer's forearm? kg · m2

Answer 1

`0.496 kg m^2`

Step-by-step explanation:

The torque exerted is given by

`\tau = Fd`

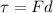
where

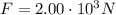`F=2.00 \cdot 10^3 N` is the force applied

d = 3.10 cm = 0.031 m is the length of the lever arm

Substituting,

`\tau=(2.00\cdot 10^3 N)(0.031 m)=62 Nm`

The equivalent of Newton's second law for rotational motion is:

`\tau = I \alpha`

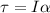
where

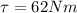`\tau = 62 Nm` is the net torque

I is the moment of inertia

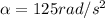`\alpha = 125 rad/s^2` is the angular acceleration

Solving the equation for I, we find

`I=(\tau)/(\alpha)=(62 Nm)/(125 rad/s^2)=0.496 kg m^2`