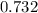Question

Solve. 90
`x` = 27.

Answer 1

Answer:
`x`≈
`0.732`

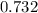
Explanation:

You need to find the value of the variable "x".

To solve for "x" you need to apply the following property of logarithms:

`log(m)^n=nlog(m)`

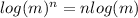
Apply logarithm on both sides of the equation:

`90^x=27\\\\log(90)^x=log(27)`

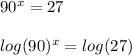
Now, applying the property mentioned before, you can rewrite the equation in this form:

`xlog(90)=log(27)`

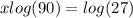
Finally, you can apply the Division property of equality, which states that:

`If\ a=b,\ then\ (a)/(c)=(b)/(c)`

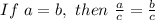
Therefore, you need to divide both sides of the equation by
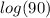`log(90)`. Finally, you get:

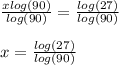
`(xlog(90))/(log(90))=(log(27))/(log(90))\\\\x=(log(27))/(log(90))`

`x`≈
`0.732`