A 50 g ball of clay traveling at speed v0 hits and sticks to a 1.0 kg block sitting at rest on a frictionless surface. A) What is the speed of the block after the collision? B) …

Question

asked Nov 21, 2020 173k views

1 Answer

Gopal · Answer 1 · 2020-11-26T10:41:42+0000

A)

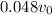
The law of conservation of momentum states that the total initial momentum must be equal to the total final momentum, so

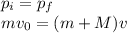
$p_i = p_f\\m v_0 = (m+M)v$

where

m = 50 g = 0.05 kg is the mass of the ball

v0 is the initial speed of the ball

M = 1.0 kg is the mass of the block

v is the final speed of the block+ball together

Solving for v, we find

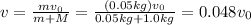
v=(mv_0)/(m+M)=((0.05 kg)v_0)/(0.05 kg+1.0 kg)=0.048 v_0

B) 95.2 %

The initial kinetic energy of the ball is:

K_i=(1)/(2)mv_0^2 = (1)/(2)(0.05 kg)v_0^2 = 0.0250 v_0^2

while the final kinetic energy of the system is

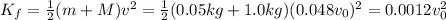
K_f=(1)/(2)(m+M)v^2 = (1)/(2)(0.05 kg+1.0 kg)(0.048 v_0)^2 = 0.0012 v_0^2

So, the loss in kinetic energy is

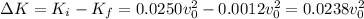
$\Delta K=K_i - K_f = 0.0250 v_0^2 - 0.0012 v_0 ^2 =0.0238 v_0^2$

In percentage,

$(\Delta K)/(K_i)=(0.0238 v_0^2)/(0.0250 v_0^2)=0.952$

which means 95.2%.