Question

What is the following difference 11 square root 45 -4 square root 5

Answer 1

Your problem looks like this

`11√(45)  - 4√(5)`

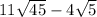
To make this problem easier, we need to simplify these square roots

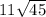`11√(45)` can be simplified

Here's how :

The factors of 45 are 9 and 5

9 is a perfect square root, but 5 is not

Think of the problem like this

`√(9)     ×     √(5)`

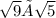
The square root of 9 is 3, but 5 has no perfect square root

Now
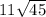`11√(45)` is simplified to
`33√(5)`

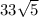
Now let's solve the problem, because we have a common square root of 5

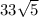`33√(5)` - 4\sqrt{5}[/tex]

Our final answer is

`29√(5)`

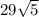
Feel free to ask questions if you are confused! Hope I helped :)

Answer 2

For this case we must simplify the following expression:

`11 \sqrt {45} -4 \sqrt {5}`

So, we rewrite 45 as
`3 ^ 2 * 5`:

`11 \sqrt {3 ^ 2 * 5} -4 \sqrt {5} =`

We have by definition of properties of powers and roots that:

`\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}`

So:

`11 * 3 \sqrt {5} -4 \sqrt {5} =\\33 \sqrt {5} -4 \sqrt {5} =\\29 \sqrt {5}`

Answer:

`29 \sqrt {5}`