Answer:
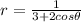
Explanation:
Let us write the equations in standard form:

We have
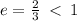 and
and

Since the eccentricity of this conic is less than 1, the conic represents an ellipse.
The second equation is
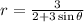 .
.
This is a hyperbola, because eccentricity is more than 1.
The third equation is
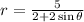 .
.
This is a parabola, because eccentricity is 1.
The fourth equation is
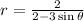 .
.
This is also a hyperbola, because eccentricity is more than 1.