Question

Megan drove from her house to work at an average speed of 45 miles per hour. The drive took her

20 minutes. If the drive home took her 30 minutes and she used the same route in reverse, what was her average speed going home?

Answer 1

30

Explanation:

Since the question says that it took her 45 minutes per hour, you can use that to find the distance of the route she took.

45 miles: 60 minutes

15 miles: 20 minutes ----------------cross multiply (20x45 and then divide by 60)

Therefore, if she is going to use the same route in reverse, the distance would be 15 miles.

Use the formula for speed:

speed= distance/time

= 15/0.5 ---------- 0.5 hours is the same as 30 minutes

= 30

Answer 2

First option: 30 miles per hour

Explanation:

For the first scenario, we will convert the minutes into hours first to get all the quantities in same unit

So,

20 minutes = 1/3 hours = 0.33 hours

Now using the speed, distance and time formula

Speed = distance/time

`Speed = (distance)/(time)`

`45 = (distance)/((1)/(3) )`

`45 = 3 * distance`
`(45)/(3) = Distance`

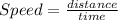
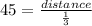
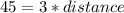
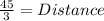
So the distance is 15 miles.

For returning through the same route

Time = 30 minutes = 0.5 hour

Distance = 15 miles

So,

`speed = (distance)/(time)`

`Speed = (15)/(0.5)`

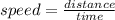
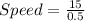
Speed = 30 miles per hour

So first option is correct..