Question

Due to ever-changing technology, a new XYZ Smartphone decreases in value 20% each year.

1. How much will this $1000 phone be worth in 2 years?

2. How long until it is worth less than 10% of it's original price?

Answer 1

1. $640

2. About 10.3 years later

Explanation:

This is a compound decay problem. The formula is

`F=P(1-r)^t`

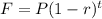
Where

F is the future amount

P is the initial amount

r is the rate of decrease (in decimal), and

t is the time in years

Question 1:

We want to find F after 2 years of a phone initially costing 1000. So,

P = 1000

r = 20% or 0.2

t = 2

plugging into the formula, we solve for F:

`F=P(1-r)^t\\F=1000(1-0.2)^2\\F=1000(0.8)^2\\F=640`

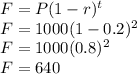
The phone is worth $640 after 2 years

Question 2:

We want to find when will the phone be worth 10% of original.

10% of 1000 is 0.1 * 1000 = 100

So, we want to figure this out for future value of 100, so F = 100

We know, P = 1000 r = 0.2 and t is unknown.

Let's plug in and solve for t (we need to use logarithms):

`F=P(1-r)^t\\100=1000(1-0.2)^t\\100=1000(0.8)^t\\(100)/(1000)=0.8^t\\0.1=0.8^t\\ln(0.1)=ln(0.8^t)\\ln(0.1)=t*ln(0.8)\\t=(ln(0.1))/(ln(0.8))\\t=10.32`

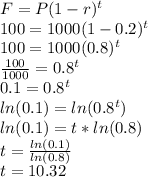
So, after 10.32 years, the phone would be worth less than 10% of original value.