Answer:
John will get more money after 5 years.
Explanation:
To calculate compound interest we use the formula
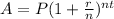
A = Amount
P = Principal
r = Rate of interest ( in decimal )
n = number of compounding period (quarterly = 4) (monthly = 12)
t = time in years
John wants to deposit $1000 with an interest of 4% compounded quarterly for 5 years.
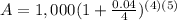
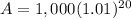
A = 1000 ( 1.22019 )
A = $1220.19
John will get $220.19 as interest after 5 years.
Cayden wants to deposit $1,000 with an interest of 3% compounded monthly for 5 years.
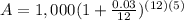
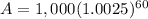
A = 1,000 ( 1.161617 )
A = 1161.62
Cayden will get $161.62 as interest after 5 years.
Therefore, John will get more money after 5 years.