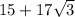First of all, let's make the following observations:
15 is an integer, so in particular it is rational. The sum of two rational is rational. This means that
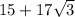 is irrational if and only if
is irrational if and only if
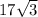 is irrational.
is irrational.
Similarly, since 17 is rational and the multiplication of two rationals is rational, we have that
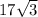 is irrational if and only if
is irrational if and only if
 is irrational.
is irrational.
The proof that
 is irrational is the following: suppose by contradiction that we could write
is irrational is the following: suppose by contradiction that we could write
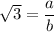
where a and b are two integers with no common factors.
Squaring both sides, we have
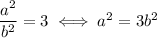
So,
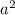 is a multiple of 3. This happens if and only if a itself is a multiple of 3. So, we can write
is a multiple of 3. This happens if and only if a itself is a multiple of 3. So, we can write
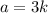 and the expression becomes
and the expression becomes
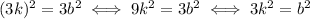
So,
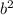 is a multiple of 3 as well, and this happens if and only if b is itself a multiple of 3.
is a multiple of 3 as well, and this happens if and only if b is itself a multiple of 3.
So, we started with the assumption that we could write
 as a reduced fraction, but this assumption led to a contradiction.
as a reduced fraction, but this assumption led to a contradiction.
We deduce that
 is irrational, and so are
is irrational, and so are
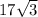 and
and