Question

Calculate the number of moles of an ideal gas if it occupies 1750 dm3 under 125,000 Pa at a temperature of 127 C.

Answer 1

65.81

Step-by-step explanation:

Educere/ Founder's Education

Answer 2

Hello!

The answer is:

The number of moles (n) is 65.55 mol.

`n=65.55mol`

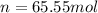
Why?

To solve the problem, we need to use the ideal gas law.

The Ideal Gas Equation is given by the following expression:

`PV=nRT`

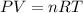
Where,

P, is the pressure in atm

V, is the volume in liters (L)

n, is the number of moles

R, is the Ideal Gas Constant

T, is the temperature in Kelvin (K)

We are given the information:

`P=12500Pa\\V=1750dm^(3)\\T=127\°C`

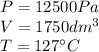
We need to convert the given units in order to use the Ideal Gas Equation, so, converting we have:

Pressure:

We know that:

`1atm=101325Pa`

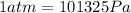
So, converting we have

`125000Pa*(1atm)/(101325Pa)=1.23atm`

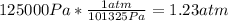
Volume:

We know that:

`1L=1dm^(3)`

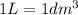
So, we have:

`1750dm^(3)=1750L`

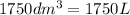
Temperature:

We know that to convert from celsius degrees to Kelvin, we need to perform the following operation:

`T(K)=T(\°C)+273.15`

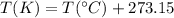
So, converting we have:

`T(K)=127+273.15=400.15`

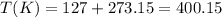
Also, we have that

`R=0.08205746(atm.L)/(mol.K)`

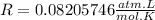
Now, substituting the given information into the equation to isolate "n", we have:

`PV=nRT\\\\1.23atm*1750L=n*0.08205746(atm.L)/(mol.K)*400.15K\\\\2152.5atm.L=n*32.84(atm.L)/(mol)\\\\n=(2152.5atm.L)/(32.84atm.L)mol\\\\n=65.55mol`

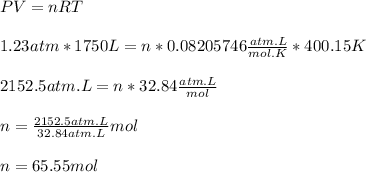
Hence, we have that the number of moles (n) is 65.55 mol.

Have a nice day!