Answer:
Total area equation = tex]w(w+6)=91[/tex]
b/2 = 3
Dimensions of the patio: width = 7 feet, length = 13 feet
Explanation:
The area of a rectangle is given the formula:
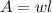
where
 is the width
is the width
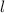 is the length
is the length
We know from our problem that the area of the patio is 91 square feet, so
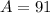 . We also know that the length is 6 feet longer then the width, so
. We also know that the length is 6 feet longer then the width, so
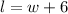 .
.
Replacing values in our area equation
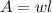
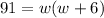

Expanding the left side:


Remember that to complete the square we need to add half the coefficient of the linear term squared. The lineal term is
 , so its coefficient is 6. Now, half its coefficient or
, so its coefficient is 6. Now, half its coefficient or
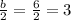 . Finally,
. Finally,
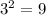 .
.
To complete the square we need to add 9 to both sides of the equation:
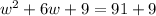
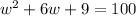
Notice that the left side is a perfect square trinomial (both
 and 9 are perfect squares), so we can express it as:
and 9 are perfect squares), so we can express it as:
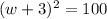
Now that we completed the square, we can solve our equation
- Take square root to both sides

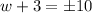
- Subtract 3 from both results
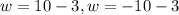
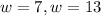
Since length cannot be negative,
 is the solution of our equation.
is the solution of our equation.
We now know that the width of our rectangular patio is 7 feet, so we can find its length:
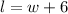
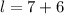
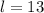
We can conclude that half the coefficient of the width is
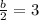 , the width of the patio is 7 feet, and its length is 13 feet.
, the width of the patio is 7 feet, and its length is 13 feet.