Question

What is the perimeter and area of a triangle?
J(-5,6). K(3,4) L(-2,1)

Answer 1

Perimeter of triangle JKL:
`2 √(17) + 2√(34)`.

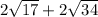Area of triangle JKL: 17.

Explanation:

None of the three sides of triangle JKL is parallel to either the x-axis or the y-axis. Apply the Pythagorean Theorem to find the length of each side.

`\rm JK = \sqrt{(3 - (-5))^(2) + (4- 6)^(2)} = \sqrt{8^(2) + (-2)^(2)} = √(68) = 2√(17)`.

`\rm JL = \sqrt{(-2 - (-5))^(2) + (1- 6)^(2)} = \sqrt{3^(2) + (-5)^(2)} = √(34)`.

`\rm KL = \sqrt{(-2 - 3)^(2) + (1-4)^(2)} = \sqrt{(-5)^(2) + (-3)^(2)} = √(34)`.

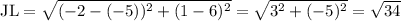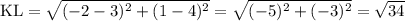The perimeter of triangle JKL will be:

`\rm JK + JL + KL = 2√(17) + √(34) + √(34) = 2 √(17) + 2√(34)`.

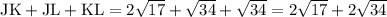Finding the Area of JKL:

Method One

In case you realized that
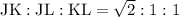`\rm JK : JL : KL = √(2) : 1 : 1`, which makes JKL an isosceles right triangle:

Area of a right triangle:

`\begin{aligned}\displaystyle \rm Area &= (1)/(2) * \text{First Leg} * \text{Second Leg}\\ &=(1)/(2) * √(34)*√(34)\\&= 17\end{aligned}`.

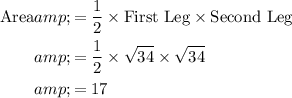Method Two

Alternatively, apply the Law of Cosines to find the cosine of any of the three internal angles. This method works even if the triangle does not contain a right angle.

Taking the cosine of angle K as an example:

`\displaystyle\begin{aligned}\rm cos(K)&=\frac{(\text{First Adjacent Side})^(2) + (\text{Second Adjacent Side})^(2)-(\text{Opposite Side})^(2)}{2* (\text{First Adjacent Side})*(\text{Second Adjacent Side})}\\&\rm =((JK)^(2) + (JL)^(2) -(KL)^(2))/(2* JK * JL)\\&=((2√(17))^(2)+(√(34))^(2)-(√(34))^(2))/(2*√(34) *(2√(17)))\\ &=(2^(2)* 17)/(2* √(2)*√(17)* 2* √(17))\\&=(1)/(√(2))\end{aligned}`.

Apply the Pythagorean Theorem to find the sine of angle K:

`\displaystyle \rm sin(K) = \sqrt{1 - (cos(K))^(2)} = \sqrt{1 - \left((1)/(√(2))\right)^(2) } = \sqrt{(1)/(2)} = (1)/(√(2)) = (√(2))/(2)`.

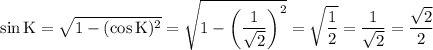The height of JKL on the side JK will be:

`\displaystyle \rm KL \cdot sin(K) = √(34) * (√(2))/(2) = (√(68))/(2) = (2√(17))/(2) = √(17)`.

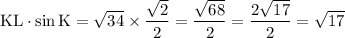What will be the area of JKL given its height
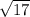`√(17)` on a base of length
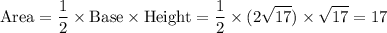`2√(17)`?

`\displaystyle \rm Area = (1)/(2) * Base* Height = (1)/(2)* (2√(17))* √(17) = 17`.