Answer:
x = 0
Explanation:
Since the product is not equal zero, we need to multiply both parenthesis first:
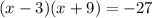
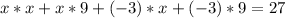
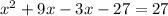
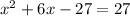
Add 27 from both sides:
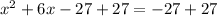
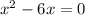
Factor
 out:
out:
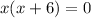
Apply the zero product:
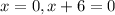
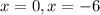
The solutions of the equation are
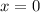 and
and
 .
.
We can conclude that the correct answer is x = 0.