Question

A ball is shot into the air using a brand new super-high-tech robotic arm to help baseball players practice catch fly balls.

The ball has an initial upward velocity of 64 feet per second. The height, h, of the ball after t seconds is given by the
equation:

​

Answer 1

69 feet

Explanation:

we have

`h(t)=-16t^(2)+64t+5`

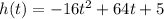
where

h(t) is the height of the ball

t is the time in seconds

we know that the given equation is a vertical parabola open downward

The vertex is the maximum

so

the y-coordinate of the vertex represent the maximum height of the ball

Convert the quadratic equation into vertex form

The equation in vertex form is equal to

`y=(x-h)^(2)+k`

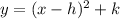
where

(h,k) is the vertex of the parabola

`h(t)=-16t^(2)+64t+5`

`h(t)-5=-16t^(2)+64t`

`h(t)-5=-16(t^(2)-4t)`

`h(t)-5-64=-16(t^(2)-4t+4)`

`h(t)-69=-16(t^(2)-4t+4)`

`h(t)-69=-16(t-2)^(2)`

`h(t)=-16(t-2)^(2)+69`

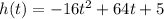
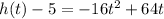
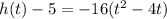
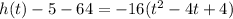
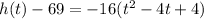
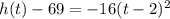
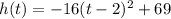
the vertex is the point (2,69)

therefore

The maximum height is 69 ft