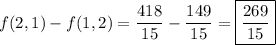Question

83

1 Show that I= {xy²w² dx + x²yw² dy + x²y²w dw} is independent of
the path of integration c and evaluate the integral from A (1, 3, 2) to
B (2, 4, 1).
2 Determine whether dz= 3x²(x² + y2) dx + 2y(x3 + y) dy is an exact
differential. If so, determine z and hence evaluate fedz from A (1, 2)
to B (2, 1).

Answer 1

1. Observe that

`\\abla \frac{x^2y^2w^2}2 = \langle xy^2w^2, x^2yw^2, x^2y^2w\rangle`

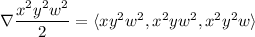
is a gradient field, so the gradient theorem holds and the integral in question is indeed path-independent. Its value is

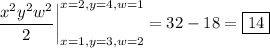
`\frac{x^2y^2w^2}2\bigg|_(x=1,y=3,w=2)^(x=2,y=4,w=1) = 32 - 18 = \boxed{14}`

2.
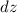`dz` is an exact differential if we can find a scalar function
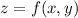`z=f(x,y)` such that

`(\partial f)/(\partial x) = 3x^2 (x^2+y^2) = 3x^4 + 3x^2y^2`

`(\partial f)/(\partial y) = 2y(x^3+y) = 2x^3y + 2y^2`

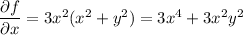
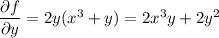
Integrating both sides of the first equation with respect to
`x` yields

`f(x,y) = \frac35 x^5 + x^3 y^2 + g(y)`

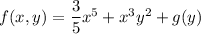
Differentiating with respect to
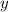`y` gives

`(\partial f)/(\partial y) = 2x^3y + (dg)/(dy) = 2x^3y + 2y^2 \\\\ \implies (dg)/(dy) = 2y^2 \implies g(y) = \frac23y^3 + C`

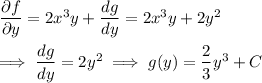
and we ultimately find

`f(x,y) = \boxed{z = \frac35 x^5 + x^3y^2 + \frac23 y^3 + C}`

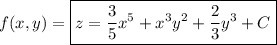
(We can also use the same method here to determine the scalar function in part (1).)

Then the integral is path-independent, and its value is

`f(2,1) - f(1,2) = (418)/(15) - (149)/(15) = \boxed{(269)/(15)}`