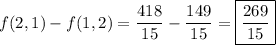1. Observe that
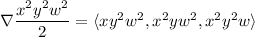
is a gradient field, so the gradient theorem holds and the integral in question is indeed path-independent. Its value is
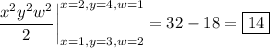
2.
 is an exact differential if we can find a scalar function
is an exact differential if we can find a scalar function
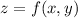 such that
such that
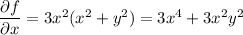

Integrating both sides of the first equation with respect to
 yields
yields
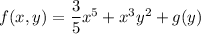
Differentiating with respect to
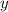 gives
gives
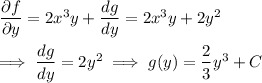
and we ultimately find
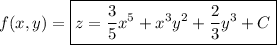
(We can also use the same method here to determine the scalar function in part (1).)
Then the integral is path-independent, and its value is