Question

Consider the graph of the line y = x – 4 and the point (−4, 2).

The slope of a line parallel to the given line is
.
A point on the line parallel to the given line, passing through (−4, 2), is .
The slope of a line perpendicular to the given line is .
A point on the line perpendicular to the given line, passing through (−4, 2), is .

Answer 1

a. The slope of a line parallel to the given line is 1

b. A point on the line parallel to the given line, passing through (−4, 2), is (1,7)

c. The slope of the line perpendicular to the given line is -1

d. A point on the line perpendicular to the given line, passing through (−4, 2), is (3,-5)

Explanation:

The equation of the line in Slope-intercept form is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

a. For the line
`y = x - 4`

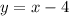
You can identify that:

`m=1`

By definition, two lines are parallel if they have the same slope. Then, the slope of a line parallel to the given line is:

`m=1`

b. The equation of the line in Point-slope form is:

`y -y_1 = m(x - x_1)`

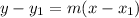
Where m is the slope and (
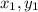`x_1,y_1`) is a point of the line.

Given the point (-4,2), substitute this point and the slope of the line into the equation:

`y -2 = (x +4)`

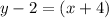
Give a value to "x", substitute it into this equation and solve for "y":

For
`x=1` :

`y -2 = (1 +4)`

`y= 5+2`

`y= 7`

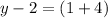
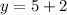
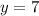
Then, you get the point (1,7)

c. The slopes of perpendicular lines are negative reciprocals, then the slope of a line perpendicular to the given line is:

`m=-(1)/(1)\\\\m=-1`

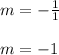
d. Given the point (-4,2), substitute this point and the slope of the line into the equation:

`y -2 = -1(x +4)`

`y -2 = -(x +4)`

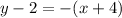
Give a value to "x", substitute it into this equation and solve for "y":

For
`x=3` :

`y -2 = -(3 +4)`

`y= -7+2`

`y= -5`

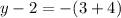
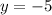
Then, you get the point (3,-5)