Question

Jane had 275 stickers, which she gave to her friends. Each friend got five more stickers than the friend before. If the first friend got 5 stickers, how many friends got stickers from Jane?

Answer 1

10 friends

Explanation:

we know that

The formula of the sum is equal to

`sum=(n)/(2)[2a1+(n-1)d]`

where

a1 is the first term

n is the number of terms (number of friends)

d is the common difference in the arithmetic sequence

In this problem we have

`sum=275\ stickers`

`a1=5\ stickers`

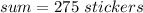
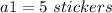
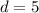`d=5` ----> the common difference

substitute in the formula and solve for n

`275=(n)/(2)[2(5)+(n-1)(5)]`

`550=n[10+5n-5]\\ \\550=10n+5n^(2) -5n\\ \\5n^(2)+5n-550=0`

Solve the quadratic equation by graphing

The solution is n=10

see the attached figure

therefore

She had 10 friends who got stickers