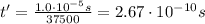a. 37500; 299,792,457.9 m/s
The formula for the length contraction for a particle moving close to the speed of light is:
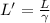
where
L' is the length observed by the particle moving
L is the length observed by an observer at rest
In this problem, we have
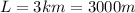 is the length of the SLAC measured by an observer at rest
is the length of the SLAC measured by an observer at rest
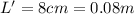 is the length measured by the electrons moving
is the length measured by the electrons moving
Substituting into the formula, we find the gamma factor
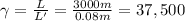
The formula for the gamma factor is
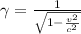
where v is the electron's speed and c is the speed of light. Re-arranging the equation, we find v:
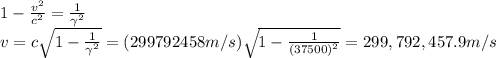
b.
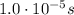
For an observer at rest in the laboratory, the electron is moving at a speed of
v = 299,792,457.9 m/s
and it covers a total distance of
L = 3000 m
which is the length of the SLAC measured by the observer. Therefore, the time it takes for the electron to travel down the tube is

c.
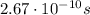
From the electron's point of view, the length of the SLAC is actually contracted, so the electron "sees" a total distance to cover of
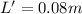
And this means that the total time of travel of the electron, in its frame of reference will be shorter; in particular it is given by the formula:
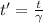
where
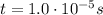 is the time measured by the observer at rest
is the time measured by the observer at rest
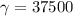
Substituting,