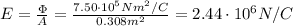Question

A circular loop of wire with a diameter of 0.626 m is rotated in a uniform electric field to a position where the electric flux through the loop is a maximum. At this position, the electric flux is 7.50 × 105 N⋅m2/C. Determine the magnitude of the electric field. A) 8.88 × 105 N/C B) 1.07 × 106 N/C C) 2.44 × 106 N/C D) 4.24 × 106 N/C E) 6.00 × 106 N/C

Answer 1

C) 2.44 × 106 N/C

Step-by-step explanation:

The electric flux through a circular loop of wire is given by

`\Phi = EA cos \theta`

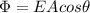
where

E is the electric field

A is the cross-sectional area

`\theta` is the angle between the direction of the electric field and the normal to A

The flux is maximum when
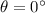`\theta=0^(\circ)`, so we are in this situation and therefore
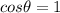`cos \theta =1`, so we can write

`\Phi = EA`

Here we have:

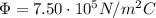`\Phi = 7.50\cdot 10^5 N/m^2 C` is the flux

d = 0.626 m is the diameter of the coil, so the radius is

r = 0.313 m

and so the area is

`A=\pi r^2 = \pi (0.313 m)^2=0.308 m^2`

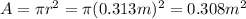
And so, we can find the magnitude of the electric field:

`E=(\Phi)/(A)=(7.50\cdot 10^5 Nm^2/C)/(0.308 m^2)=2.44\cdot 10^6 N/C`