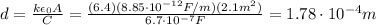Answer:
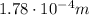
Step-by-step explanation:
The capacitance of the capacitor is given by:
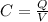
where
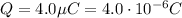 is the charge stored on the plates
is the charge stored on the plates
V = 6.0 V is the potential difference across the capacitor
Substituting, we find

The capacitance of a parallel-plate capacitor is also given by
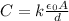
where
k = 6.4 is the dielectric constant
 is the vacuum permittivity
is the vacuum permittivity
 is the area of each plate
is the area of each plate
d is the separation between the plates
Solving for d, we find