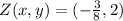Answer:
Explanation:
Point Z divides XY into a 5:3 ratio, so Z is 5/3 of the way from X to Y. That ratio is k, found by writing the numerator of the ratio (5) over the sum of the numerator and the denominator (5 + 3 = 8). Our k value is 5/8. Now we will find the rise and run values which is the slope of this line segment:
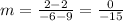
Coordinates are found in this formula:
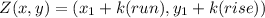
Filling that in:
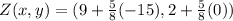
which simplifies to

which gives us the final coordinates of Z to be