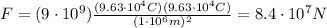Question

One mole of a substance contains 6.02 × 1023 protons and an equal number of electrons. If the protons could somehow be separated from the electrons and placed in very small, individual containers separated by a million meters, what would be the magnitude of the electrostatic force exerted by one box on the other? A) 8.7 × 103 N B) 9.5 × 104 N C) 2.2 × 105 N D) 8.4 × 107 N E) 1.6 × 108 N

Answer 1

`8.4\cdot 10^7 N`

Step-by-step explanation:

The electrostatic force between two objects is given by:

`F=k(q_1 q_2)/(r^2)`

where

k is the Coulomb's constant

q1 and q2 are the charges of the two objects

r is the separation between the two objects

In this problem, we have two boxes separated by

`r = 1\cdot 10^6 m`

The first box contains
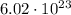`6.02\cdot 10^(23)` protons, so its charge is:

`q_1 = (6.02\cdot 10^(23))(1.6\cdot 10^(-19) C)=9.63\cdot 10^4 C`

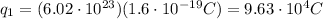
The second box contains
`6.02\cdot 10^(23)` electrons, so its charge is:

`q_2 = (6.02\cdot 10^(23))(-1.6\cdot 10^(-19) C)=-9.63\cdot 10^4 C`

We are only interested in the magnitude of the force, so we can neglect the negative sign and calculate the electrostatic force as:

`F=(9\cdot 10^9) ((9.63\cdot 10^4 C)(9.63\cdot 10^4 C))/((1\cdot 10^6 m)^2)=8.4\cdot 10^7 N`