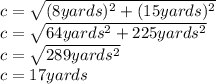Question

Sondra wants to put a fence in a triangular area of her backyard as shown in the illustration. The fence will enclose a right triangle, with two of the sides measuring 8 yards and 15 yards long. How long will the third side of the triangle be?

(the question did not contain an illustration)

Answer 1

17 yds

Explanation:

Lacking further info about this situation, I will assume that 8 yards and 15 yards represent the two legs of this right triangle, and not the hypotenuse. If that's the case, then the hypotenuse is found by applying the Pythagorean Theorem:

(8 yd)² + (15 yd)² = hyp², or

64 yd² + 225 yd² = 289 yd²

Taking the square root of this result yields 17 yds.

The third side will be 17 yds long.

Answer 2

17 yards. The fence that enclose Sondra's backyard is a right triangle whose sides measuring 8 yards, 15 yards and 17 yards respectively.

The key to solve this problem is using the Pythagorean Theorem that dictates; In every right triangle the square of the hypotenuse is equal to the sum of the squares of the legs and the equation hypotenuse²=leg1²+leg2².

For this problem we know the measuring of two side, which mean that we can apply Pythagorean Theorem equation as follow:

Let's say that one of the side is a = 8yards, and the other side is b = 15yards. So, we want to know how long the third side c long.

Applying the Pythagorean Theorem:

`c^(2) =a^(2)+b^(2)  \\c=\sqrt{a^(2)+b^(2)}`

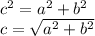
Substituting the values of the sides a and b:

`c=\sqrt{(8yards)^(2)+(15yards)^(2)}\\c=\sqrt{64yards^(2)+225yards^(2)}\\c=\sqrt{289yards^(2)}\\c=17yards`