Question

PLEASE HELP!!

In isosceles △ABC, AB = BC and CH is an altitude. Find the perimeter of △ABC, if CH = 84 cm and m∠HBC = m∠BAC +m∠BCH?

Answer 1

I think I could help you

Have fun and feel free to ask me something new.

Or we can prove some properities without calculating by details

Explanation:

I think I could help you

Have fun and feel free to ask me something new.

Or we can prove some properities without calculating by details

Answer 2

Answer: The perimeter of triangle ABC is (112√3 + 168) cm.

Step-by-step explanation: Given that in isosceles triangle △ABC, AB = BC and CH is an altitude. Also,

CH = 84 cm and

`m\angle HBC = m\angle BAC+m\angle BCH~~~~~~~~~~~~~~~~~~~~~~~(i)`

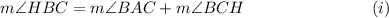
We are to find the perimeter of triangle ABC

Since AB = BC, so the angles opposite to them are congruent and have equal measures.

That is,
`m\angle BAC=m\angle ACB~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

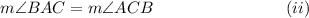
Now, since angle HBC is an exterior angle of triangle ABC and triangles BAC and ACB are remote interior angles.

So, we have

`m\angle HBC=m\angle BAC+m\angle ACB\\\\\Rightarrow m\angle BAC+m\angle BCH=m\angle BAC+m\angle ACB\\\\\Rightarrow m\angle ACB=m\angle BCH.`

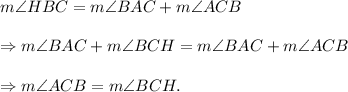
Therefore, from equation (i) implies that

`m\angle HBC = m\angle BAC+m\angle BCH\\\\\Rightarrow m\angle HBC=m\angle BCH+m\angle BCH~~~~~~~[\textup{applying equations (ii) and (iii)}]\\\\\Rightarrow m\angle HBC=2m\angle BCH.`

Now, from angle sum property in triangle BCH, we have

`m\angle HBC+m\angle BCH+m\angle BHC=180^\circ\\\\\Rightarrow 3m\angle BCH+90^\circ=180^\circ\\\\\Rightarrow 3m\angle BCH=90^\circ\\\\\Rightarrow m\angle BCH=30^\circ.`

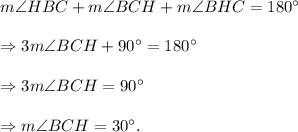
So, we get

`m\angle BAC=m\angle ACB=m\angle BCH=30^\circ,\\\\m\angle HBC=2*30^\circ=60^\circ.`

In right-angled triangle ACH, we have

`\tan 30^\circ=(CH)/(AH)\\\\\\\Rightarrow (1)/(\sqrt3)=(84)/(AH)\\\\\\\Rightarrow AH=84\sqrt3.`

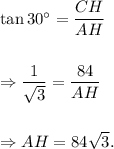
In right-angled triangle BCH, we have

`\tan 60^\circ=(CH)/(BH)\\\\\\\Rightarrow \sqrt3=(84)/(BH)\\\\\\\Rightarrow BH=(84)/(\sqrt3).`

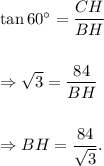
And,

`\sin 60^\circ=(CH)/(BC)\\\\\\\Rightarrow (\sqrt3)/(2)=(84)/(BC)\\\\\\\Rightarrow BC==(168)/(\sqrt3)=56\sqrt3.`

Therefore,

`AB=AH-BH=84\sqrt3-(84)/(\sqrt3)=\sqrt3(84-28)=56\sqrt3.`

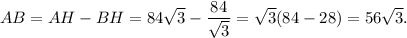
Now, in triangle ACH,

`\sin 30^\circ=(CH)/(AC)\\\\\\\Rightarrow (1)/(2)=(84)/(AC)\\\\\Rightarrow AC=168.`

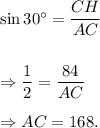
Thus, the perimeter of triangle ABC is given by

`P=AB+BC+CA=56\sqrt3+56\sqrt3+168=112\sqrt3+168.`

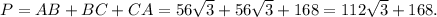
The perimeter of triangle ABC is (112√3 + 168) cm.