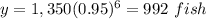Question

The fish population of Lake Collins is decreasing at a rate of 5% per year. In 2004 there were about 1,350 fish. Write an exponential decay function that models this situation. Then find the population in 2010.

Answer 1

Part 1) The exponential function is equal to
`y=1,350(0.95)^(x)`

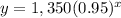
Part 2) The population in 2010 was
`992\ fish`

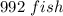
Explanation:

Part 1) Write an exponential decay function that models this situation

we know that

In this problem we have a exponential function of the form

`y=a(b)^(x)`

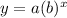
where

y ----> the fish population of Lake Collins since 2004

x ----> the time in years

a is the initial value

b is the base

we have

`a=1,350\ fish`

`b=(100\%-5\%)=95\%=0.95`

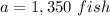
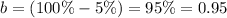
substitute

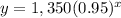`y=1,350(0.95)^(x)` ----> exponential function that represent this scenario

Part 2) Find the population in 2010

we have

`y=1,350(0.95)^(x)`

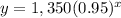
so

For
`x=(2010-2004)=6\ years`

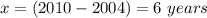
substitute

`y=1,350(0.95)^(6)=992\ fish`