Answer:
3u - 2v + w = 69i + 19j.
8u - 6v = 184i + 60j.
7v - 4w = -128i + 62j.
u - 5w = -9i + 37j.
Explanation:
Note that there are multiple ways to denote a vector. For example, vector u can be written either in bold typeface "u" or with an arrow above it
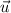 . This explanation uses both representations.
. This explanation uses both representations.
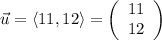 .
.
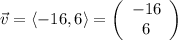 .
.
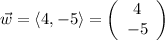 .
.
There are two components in each of the three vectors. For example, in vector u, the first component is 11 and the second is 12. When multiplying a vector with a constant, multiply each component by the constant. For example,
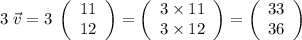 .
.
So is the case when the constant is negative:
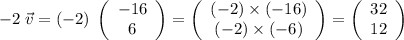 .
.
When adding two vectors, add the corresponding components (this phrase comes from Wolfram Mathworld) of each vector. In other words, add the number on the same row to each other. For example, when adding 3u to (-2)v,
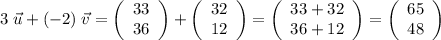 .
.
Apply the two rules for the four vector operations.
1.
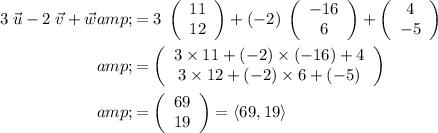
Rewrite this vector as a linear combination of two unit vectors. The first component 69 will be the coefficient in front of the first unit vector, i. The second component 19 will be the coefficient in front of the second unit vector, j.
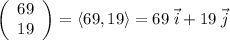 .
.
2.
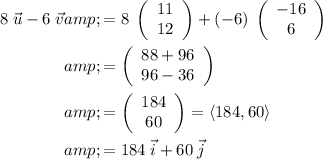 .
.
3.
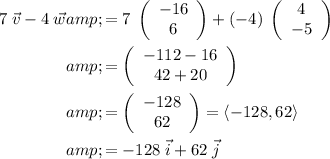 .
.
4.
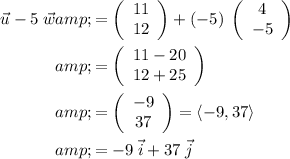 .
.