Question

The coordinates G(7,3), H(9, 0), (5, -1) form what type of polygon?

an obtuse triangle
an acute triangle
an equilateral triangle
o a right triangle

Answer 1

an acute triangle

Explanation:

Given:

vertex 1 = (7,3)

vertex 2 = (9,0)

vertex 3 = (5,-1)

Now finding the length of each side of the triangle

Using distance formula, to find the length of side between vertex 1 and 2

d=
`\sqrt{(x2-x1)^(2)+ (y2-y1)^(2) }`

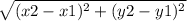
Putting values of x1=7 , x2=9, y1=3 and y2=0

d=
`\sqrt{(9-7)^(2)+ (0-3)^(2) }\\ =\sqrt{2^(2)+ 3^(2) }\\ =√(4+9) \\=√(13)`

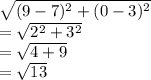
Using distance formula, to find the length of side between vertex 1 and 3

Putting values of x1=7 , x2=5, y1=3 and y2=-1

d=
`\sqrt{(5-7)^(2)+ (-1-3)^(2) }\\ =\sqrt{2^(2)+ 4^(2) }\\ =√(4+16) \\=\sqrt{20`

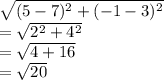
Using distance formula, to find the length of side between vertex 2 and 3

Putting values of x1=9 , x2=5, y1=0 and y2=-1

d=
`\sqrt{(5-9)^(2)+ (-1-0)^(2) }\\ =\sqrt{4^(2)+ 1^(2) }\\ =√(16+1) \\=\sqrt{17`

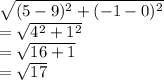
Hence the three sides of triangle are:

√13, √20, √17

by Pythagoras theorem

if c^2= a^2 + b^2 then triangle is right triangle

if c^2> a^2 + b^2 then triangle is obtuse triangle

if c^2<a^2 + b^2 then triangle is acute triangle

Now let a=√13 b=√17 and c=√20 then:

a^2 + b^2 = 13+17

= 30

c^2=20

and 20 < 30 which means c^2<a^2 + b^2 then triangle is acute triangle !