Explanation:
This is the classic example of a linear equation.
Remember this form
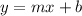 ?
?
Y is the cost of the hotel.
m is the cost per hour of the hotel.
x is the number of hours the room is rented for.
b is the initial fee.
If we are trying to find the number of hours (x) that these two hotels cost the same (y), we would set two equations equal to each other.
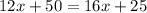
Then we can easily solve for x (the number of hours).