Answer: C.
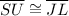
Explanation:
- SAS congruence postulate tells that if two sides and the included angle of a triangle are congruent to corresponding two sides and the included angle of other triangle, then the triangles are congruent.
In the given picture , we have two triangles ΔSTU and Δ JKL , in which we have
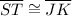

To prove ΔSTU is congruent to Δ JKL, we need
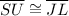 such that
such that
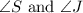 becomes congruent the included angles between pair of congruent sides.
becomes congruent the included angles between pair of congruent sides.
Hence, C is the right option.