Question

What is the solution of​

Answer 1

`x \:<\:-8` or
`x \:>\:(1)/(5)`.

Explanation:

The given inequality is
`(x+8)/(5x-1) \:>\:0`

For this statement to be true, then we must have the following cases:

Case 1

`x+8 \:<\:0\:and\:5x-1\:<\:0`

`x \:<\:-8\:and\:x\:<\:(1)/(5)`

The intersection of these two inequalities is
`x \:<\:-8`.

The solution to this first case is
`x \:<\:-8`.

Case 2

`x+8 \:>\:0\:and\:5x-1\:>\:0`

`x \:>\:-8\:and\:x\:>\:(1)/(5)`

The intersection of these two inequalities is
`x \:>\:(1)/(5)`.

The solution to this second case is
`x \:>\:(1)/(5)`.

Therefore the solution to the given inequality is

`x \:<\:-8` or
`x \:>\:(1)/(5)`.

The second option is correct

Answer 2

Hence final answer is
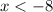`x<-8` or
`x>(1)/(5)`

correct choice is B because both ends are open circles.

Explanation:

Given inequality is
`(x+8)/(5x-1)>0`

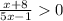
Setting both numerator and denominator =0 gives:

x+8=0, 5x-1=0

or x=-8, 5x=1

or x=-8, x=1/5

Using these critical points, we can divide number line into three sets:

`(-\infty,-8)`,
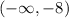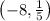`\left(-8,(1)/(5)\right)` and
`((1)/(5),\infty)`

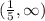
We pick one number from each interval and plug into original inequality to see if that number satisfies the inequality or not.

Test for
`(-\infty,-8)`.

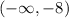Clearly x=-9 belongs to
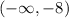`(-\infty,-8)` interval then plug x=-9 into
`(x+8)/(5x-1)>0`

`(-9+8)/(5(-9)-1)>0`

`(-1)/(-46)>0`

`(1)/(46)>0`

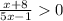
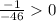
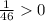
Which is TRUE.

Hence
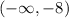`(-\infty,-8)` belongs to the answer.

Similarly testing other intervals, we get that only
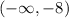`(-\infty,-8)` and
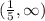`((1)/(5),\infty)` satisfies the original inequality.

Hence final answer is
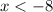`x<-8` or
`x>(1)/(5)`

correct choice is B because both ends are open circles.