Question

A container holds 22.4 L of gas at 1.00 atm and 0.0˚C.

a. Convert 0.0˚C to Kelvin.
b. State the combined gas law.
c. If the pressure increases to 1.50 atm and the temperature doesn’t change,
calculate the new volume.
d. If the temperature increases to 100.0 ˚C and the pressure doesn’t change,
calculate the new volume.

Answer 1

Step-by-step explanation:

Parameter given:

Volume of gas in the container = 22.4L

Pressure on the gas = 1.0atm

Temperature of the gas = 0.0°C

Problem 1

Coverting 0.0°C to Kelvin:

In order to convert 0.0°C to Kelvin, we apply the formula:

K = T(°C) + 273

Where T is the temperature in °C and K is the unknown temperature in Kelvin:

K = 0.0 + 273 = 273K

Problem 2

The combined gas law is also known as the general gas law. It is expressed as:

`(P_(1)V_(1)  )/(T_(1) )  = (P_(2)V_(2)  )/(T_(2) )`

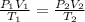
The expression combines both Boyle's law and Charle's Law.

Problem 3

Parameters given:

Volume of gas in the container V₁ = 22.4L

Pressure on the gas P₁ = 1.0atm

Temperature = 273K

P₂ = 1.50atm

Unknown: The final volume, V₂ = ?

Solution

From the given problem, we know that the temperature is constant. We apply Boyle's law. Boyle's law states that "The volume of a fixed mass of gas varies inversely a the pressure changes if the temperature is constant".

It is expressed as P₁V₁ = P₂V₂

The unknown parameter is V₂, we make it the subject of the expression:

V₂ =
`(P_(1)V_(1)  )/(P_(2) )`

V₂ =
`(1  x 22.4)/(1.5)`

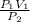
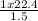
V₂ = 15L

Problem 4

The unknown here is the new volume V₂ at constant pressure.

Given parameters:

Volume of gas in the container V₁ = 22.4L

Pressure on the gas P is constant

Intial Temperature T₁ = 273K

Final Temperature T₂ = 100°C , converting to K gives, K = 100 + 273 = 373K

From the given parameters, the unknown and the conditions guiding the equation, we apply Charle's law. Charle's law states that "The volume of a fixed mass of gas is directly proportional to its absolute temperature provided pressure is constant".

it is expressed as:
`(V_(1) )/(T_(1) )  = (V_(2) )/(T_(2) )`

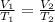
We then express the unknown V₂ as the subject of the formula:

V₂ =
`(V_(1) T_(2) )/(T_(1) )`

V₂ =
`(22.4 x 373)/(273)`

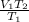
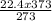
V₂ = 30.6L