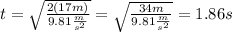Question

A spaceship hovering over the surface of Venus drops an object from a height of 17 m. How much longer does it take to reach the surface than if dropped from the same height on Earth? Neglect air resistance in both cases.

Answer 1

Step-by-step explanation:

It is given that,

A spaceship hovering over the surface of Venus drops an object from a height of 17 m, h = 17 m

Acceleration due to gravity on the surface of Venus,
`g'=8.87\ m/s^2`

The second equation of motion is given by :

`s=ut+(1)/(2)gt^2`, u = 0

`s=(1)/(2)gt^2`

`t=\sqrt{(2s)/(g')}`

`t=\sqrt{(2* 17)/(8.87)}`

t' = 1.95 s..............(1)

Acceleration due to gravity on the surface of Earth,
`g=9.8\ m/s^2`

Again using second equation of motion to find the time taken on the surface of earth.

`s=ut+(1)/(2)gt^2`, u = 0

`s=0+(1)/(2)gt^2`

`t=\sqrt{(2* 17)/(9.8)}`

t = 1.86.................(2)

Change in time,
`\Delta t=t'-t=1.95-1.86=0.089\ s`

So, on the surface of earth it will taken 0.089 seconds more. Hence, this is the required solution.

Answer 2

1.96s and 1.86s. The time it takes to a spaceship hovering the surface of Venus to drop an object from a height of 17m is 1.96s, and the time it takes to the same spaceship hovering the surface of the Earth to drop and object from the same height is 1.86s.

In order to solve this problem, we are going to use the motion equation to calculate the time of flight of an object on Venus surface and the Earth. There is an equation of motion that relates the height as follow:

`h=v_(0) t+(gt^(2))/(2)`

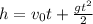
The initial velocity of the object before the dropping is 0, so we can reduce the equation to:

`h=(gt^(2))/(2)`

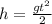
We know the height h of the spaceship hovering, and the gravity of Venus is
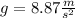`g=8.87(m)/(s^(2))`. Substituting this values in the equation
`h=(gt^(2))/(2)`:

`17m=(8.87(m)/(s^(2) ) t^(2))/(2)`

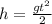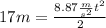
To calculate the time it takes to an object to reach the surface of Venus dropped by a spaceship hovering from a height of 17m, we have to clear t from the equation above, resulting:

`t=\sqrt{(2(17m))/(8.87(m)/(s^(2) ) )} =\sqrt{(34m)/(8.87(m)/(s^(2) ) ) }=1.96s`

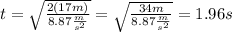
Similarly, to calculate the time it takes to an object to reach the surface of the Earth dropped by a spaceship hovering from a height of 17m, and the gravity of the Earth
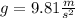`g=9.81(m)/(s^(2))`.

`t=\sqrt{(2(17m))/(9.81(m)/(s^(2) ) )} =\sqrt{(34m)/(9.81(m)/(s^(2) ) ) }=1.86s`