Question

Please find which quadratic equation matches the graph with work attached

Answer 1

C

Explanation:

Firstly, we know that the function must be negative due to its shape. This means that the answer cannot be B

Next we can use the equation
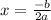`x=(-b)/(2a)` that is used in order to find the vertex of the parabola.

A)

`f(x)=-x^2+6x+7\\a=-1,b=6,c=7\\\\x=(-6)/(-2) \\x=3`

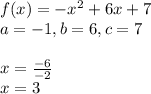
As the vertex is at x=3 on the graph, this one could be a contender.

C)

`f(x)=-x^2+6x-7\\a=-1,b=6, c=-7\\\\x=(-6)/(-2) \\\\x=3`

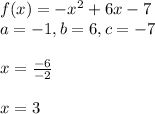
This also could be the equation

D)

`f(x)=-x^2-6x-7\\\\a=-1, b=-6, c=-7\\\\x=(6)/(-2) \\\\x=-3`

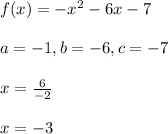
This rules option D out.

For this last step, we can look at where the zeroes would be for each equation. (These values are irrational, so we cannot look at specific number)

A)

`f(x)=-(x^2-6x-7)`

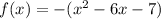
As this equation has a negative value for c, this means that one zero must be positive and the other must be negative.

This means that option A can be ruled out

C)

`f(x)=-(x^2-6x+7)`

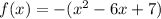
As this equation has a positive value for c, this means that both of the zeroes must be positive. This means that it is the only one that fits all of the criteria.