Question

The amount of an ordinary $9000.00 annuity for 3 years at 12 percent compounded quarterly is _______? Show Work

Answer 1

The amount after 3 years = $12381.85

Explanation:

Points to remember

Compound interest

A = P[1 +R/n]^nt

Where A - amount

P - principle amount

R = rate of interest

t - number of times compounded yearly

n number of years

To find the amount

Here,

P = $9000.00, n = 3 years, t = 4, n = 3 and R = 12% = 0.12

A = P[1 +R/n]^nt

= 9000[1 + 0.12/4]^(3 * 4)

= 9000[1 + 0.03]^12

= 12831.85

Therefore the amount after 3 years = $12381.85

Answer 2

A = $12831.8

Explanation:

We know that the formula for compound interest is given by:

`A=P((1+r)/(n) )^(nt)`

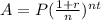
where
`A` is unknown which is the amount of investment with interest,

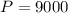`P=9000` which is the initial amount,

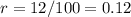`r=12/100=0.12` is the interest rate,

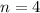`n=4` which is the number of compoundings a year; and

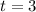`t=3` which is the number of times that interest is compounded per unit t.

So substituting these values in the above formula to find A:

`A=P((1+r)/(n) )^(nt)`

`A=9000((1+0.12)/(4) )^((4.3))`

`A = 9000(1 + 0.03)^(12)`

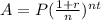
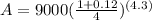
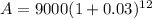
A = $12831.8