Question

Which of the following shows the extraneous solution to the logarithmic equation

x = -16
x = -4
x = 4
x = 16

Answer 1

The extraneous solution to the logarithmic equation is
`x=-4`

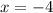
Explanation:

We have the equation:

`Log_(7) (3x^3+x)-Log_7(x)=2`

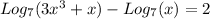
By properties of logarithms:

`LogA-LogB=Log((A)/(B))`

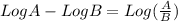
So, with the equation we have:

`Log_(7) ((3x^3+x))/(x)=2`

`Log_(7)( (3x^3+x)/(x))=2\\Log_(7)( (3x^3)/(x)+(x)/(x))=2\\Log_(7)( (3x^3)/(x)+1)=2\\Log_(7)(3x^2+1)=2`

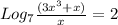
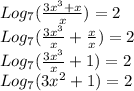
This logarithm base is 7 and this equation is equal to 2, the number 7 passes as the base on the other side of the equation and the two as an exponent, after that we just to find x:

`7^2=(3x^2+1)\\49=3x^2+1\\49-1=3x^2\\(48)/(3) =x^2\\16=x^2`

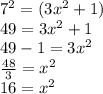
Now, we can find x with square root

`16=x^2\\√(16) =√(x^2) \\x_1=4\\x_2=-4`

This equation has two answers because it is a quadratic equation, so with this logic the strange solution is -4

Answer 2

The correct answer option is x = 4.

Explanation:

We are given the following logarithmic equation and we are to determine whether which of the given options shows its extraneous solution:

`log _ 7 ( 3 x ^ 3 + x ) - log _ 7 ( x ) = 2`

We can rewrite it as:

`log7[(3x^3+x)/(x) ]=2`

But we know that
`log_7(49)=2`

So,
`log7[(3x^3+x)/(x) ]=log_7(49)`

Cancelling the log to get:

`(3x^3+x)/(x) =49`

Further simplifying it to get:

`3x^2+1=49`

`3x^2=48`

`x^2=(48)/(3)`

`x^2=16`

x = 4