Question

Given: BD is a diameter

m 1 = 100°
m BC= 30°

m ADB=

160
280
330

Answer 1

280

Explanation:

<1=100 <4=150 <3=30

mADB=100+150+30=280

Answer 2

Answer with explanation:

Given

m∠1=100°

`m \widehat{BC}=30 ^(\circ)`

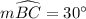
To Find:---m∠A D B

Solution

In Δ A OD

Represent the center of circle by O.

→ m∠1=100°

→OD=O A----------Radii of Circle

→∠ADO=∠D A O--------If opposite sides are equal angle opposite to them are equal.

In ΔA OD, Using Angle Sum property of Triangle

→∠ADO+∠D A O+∠A OD=180°

→2 ∠ADO+100° =180°-------------------[∠ADO=∠D A O]

→2∠ADO=180° -100°

→2∠ADO=80°

Dividing both sides by , 2 we get

⇒∠ADO=40°

⇒⇒⇒∠A DB=40°

≡⇒If you are asking about

`m \widehat{ADB}=180 ^(\circ)`

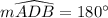
Because Angle in a semicircle is Right Angle.Diameter B D divides the circle into two equal arc measure of each arc being 180 degree.

⇒⇒If you are asking about Angle made by Major arc ADB, then

`m \widehat{ADB}=\angle AOD + \widehat{BOD}\\\\=100 ^(\circ)+180 ^(\circ)=280 ^(\circ)`

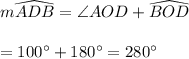
Option B