Answer:
The correct option is 2.
Explanation:
Given information:
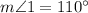 .
.
It is given that
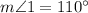 , so arc(BA)=110° and the central angle of arc BCA is
, so arc(BA)=110° and the central angle of arc BCA is
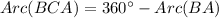
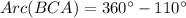
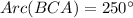
The measure of arc BC is

The measure of arc CTA is 180° because AC is the diameter.
It means options 1 and 3 are incorrect.
The measure of arc BCA is 250°. Therefore the correct option is 2.