Question

What is (x+y)(x^2-xy+y^2)

Answer 1

Hello!

The answer is:

`(x+y)(x^(2)-xy+y^(2))=x^(3)+y^(3)`

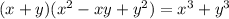
Why?

To find the resultant expression, we need to apply the distributive property.

It can be defined by the following way:

`(a+b)(c+d)=ac+ad+bc+bd`

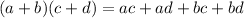
Also, we need to remember how to add like terms: The like terms are the terms that share the same variable and exponent, for example:

`x+x+x^(2)=2x+x^(2)`

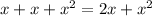
We were able to add only the two first terms since they were like terms (they share the same variable and the same exponent)

So , we are given the expression:

`(x+y)(x^(2)-xy+y^(2))`

Then, applying the distributive property, we have:

`(x+y)(x^(2)-xy+y^(2))=x*x^(2)-x*xy+x*y^(2)+y*x^(2)-y*xy+y*y^(2)\\\\x*x^(2)-x*xy+x*y^(2)+y*x^(2)-y*xy+y*y^(2)=x^(3)-x^(2)y+xy^(2)+yx^(2)-xy^(2)+y^(3)\\\\x^(3)-x^(2)y+xy^(2)+yx^(2)-xy^(2)+y^(3)=x^(3)+y^(3)`

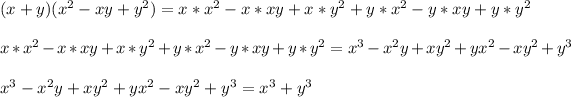
Hence, the answer is:

`(x+y)(x^(2)-xy+y^(2))=x^(3)+y^(3)`

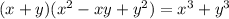
Have a nice day!