348.34 m/s. When Superman reaches the train, his final velocity will be 348.34 m/s.
To solve this problem, we are going to use the kinematics equations for constant aceleration. The key for this problem are the equations
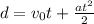 and
and
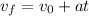 where
where
 is distance,
is distance,
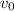 is the initial velocity,
is the initial velocity,
 is the final velocity,
is the final velocity,
 is time, and
is time, and
 is aceleration.
is aceleration.
Superman's initial velocity is
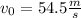 , and he will have to cover a distance d = 850m in a time t = 4.22s. Since we know
, and he will have to cover a distance d = 850m in a time t = 4.22s. Since we know
 ,
,
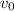 and
and
 , we have to find the aceleration
, we have to find the aceleration
 in order to find
in order to find
 .
.
From the equation
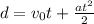 we have to clear
we have to clear
 , getting the equation as follows:
, getting the equation as follows:
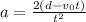 .
.
Substituting the values:
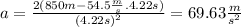
To find
 we use the equation
we use the equation
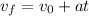 .
.
Substituting the values:
