Question

A fountain is located between two trees. Each tree has a height of 60 feet. The angles of elevation from the

base of the fountain to the top of each tree are 64° and 48° as shown below.

What is the horizontal distance between the two trees (rounded to the nearest foot)
A 40
B 837
C 147
D 190 ft

Answer 1

83 ft.

Explanation:

Just took the test :)

Answer 2

Hello!

The answer is:

The correct option is:

B) 83 feet

Why?

To solve the problem, we need to use the following trigonometric identity:

`Tan(\alpha)=(Opposite)/(Adjacent)`

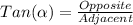
Which, translated to our problem, will be:

`Tan(\alpha)=(Height)/(Base)`

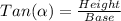
We are given two triangles, and we know their height and their angles between their hypothenuse and their bases.

So,

For the first triangle, we have:

`height=60ft\\\alpha=64\°`

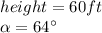
So, using the trigometric identity of the tangent, we have:

`Tan(\alpha)=(Height)/(Base)\\\\Tan(64\°)=(60ft)/(Base)\\\\Base=(60ft)/(Tan(64\°))=(60ft)/(2.05)=29.27ft`

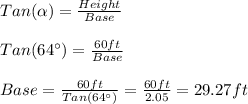
Therefore, we have that the base of the first triangle is equal to 29.27 feet.

For the second triangle, we have:

`height=60ft\\\alpha=48\°`

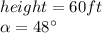
So, using the trigometric identity of the tangent, we have:

`Tan(\alpha)=(Height)/(Base)\\\\Tan(48\°)=(60ft)/(Base)\\\\Base=(60ft)/(Tan(48\°))=(60ft)/(1.11)=54.05ft`

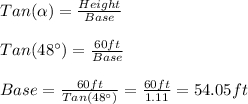
Therefore, we have that the base of the second triangle is equal to 54.05 feet.

Now, to calculate the horizontal distance between the two trees (x), we need to use the following formula with the obtained values of both triangles:

`HorizontalDistance=FirstTriangleBase+SecondTriangleBase\\\\HorizontalDistance=29.27ft+54.05=83.29ft`

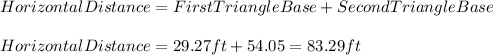
Hence, we have that the distance between the two trees rounded to the nearest foot is 83 feet.

Have a nice day!