Question

Write the equation of the circle in general form. Show your work.

Answer 1

The equation of the circle in general form is:

`\[ x^2 + y^2 = 9 \]`

The equation of a circle in the Cartesian coordinate plane is given by:

`\[ (x - h)^2 + (y - k)^2 = r^2 \]`

where
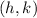`\((h, k)\)` is the center of the circle and \(r\) is the radius.

By examining the image, we can observe the following:

- The center of the circle is at the point
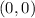`\((0, 0)\)` because the circle is centered at the origin.

- The radius of the circle is the distance from the center to any point on the circle. We can see that the circle passes through
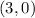`\((3, 0)\)`, so the radius
`\(r\)` is 3.

Using these observations, we can write the equation of the circle:

`\[ (x - 0)^2 + (y - 0)^2 = 3^2 \]`

`\[ x^2 + y^2 = 9 \]`

So, the equation of the circle in general form is:

`\[ x^2 + y^2 = 9 \]`

Answer 2

The equation would be:

(X+1)^2 + (y-1)^2 = 9