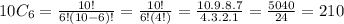Question

Permutation problem that I just do not feel like solving

Your cousin, who is planning her wedding, is working on the seating chart for the reception. She is trying to decide which 6 people should be seated at the table closest to the head table. She has narrowed her decision down to a list of 10 friends.

If the order doesn't matter, in how many ways can she choose 6 friends from the list of 10 to sit at the table closest to the head table?

Answer 1

210. she has 210 ways to choose 6 friends from the list of 10 to sit at the table closest to the head table no matter the order.

This is a problem of combinations and can be solved using the equation
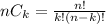`nC_(k)=(n!)/(k!(n-k)!)`, where n! and k! is the factorial of a number. The factorial is defined in principle as the product of all positive integers from 1 (ie, natural numbers) to n.

She has a list of 10 friends and we want to know in how many ways she can choose 6 friends.

Using the combinations equation, with n = 10 and k = 6:

`10C_(6)=(10!)/(6!(10-6)!)=(10!)/(6!(4!))=(10.9.8.7)/(4.3.2.1)=(5040)/(24) =210`