Question

Calculate the orbital radius of the hydrogen atom for the first principal quantum number. Use the general expression given in the test to calculate this value. (Hint: Quantum numbers are not significant digits and should not be counted as such in determining your final answer. Thus, this answer should have 2 significant digits.)

1.1
0.53
5.3

Answer 1

0.53 A

Step-by-step explanation:

Answer 2

5.3 A

Step-by-step explanation:

The orbital radius for the generic nth-level in the hydrogen atom is given by

`a_n = n^2 a_0`

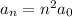
where:

`a_0 = (\epsilon_0 h^2)/(\pi m_e e^2)`

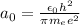
is the Bohr radius, with

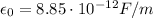`\epsilon_0 = 8.85\cdot 10^(-12) F/m` being the vacuum permittivity

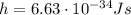`h=6.63\cdot 10^(-34)Js` is the Planck constant

`m_e = 9.11\cdot 10^(-31) kg` is the electron mass

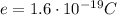`e=1.6\cdot 10^(-19) C` is the electron charge

Substituting all this numbers into the formula, we find

`a_0 = 5.3\cdot 10^(-10) m = 5.3 A`

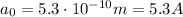
and since

n = 1

the radius of the hydrogen atom for the first principal quantum number is

`a_1 = 1^2 a_0 = 1 \cdot (5.3 A)=5.3 A`