Answer:
124.7 in²
Explanation:
A hexagon consists of six equilateral triangles, each of side a, and we can divide each of them into two right triangles.
So, we can calculate the area of one right triangle and multiply by 12.
The formula for the area of one triangle is
A = ½bh
Step 1. Calculate the length of the side a
Per the Pythagorean Theorem,
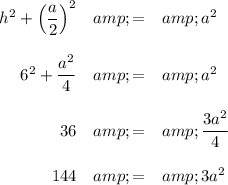
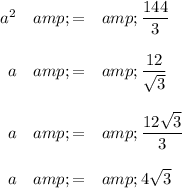
2.Calculate the area of a small triangle
The base of a small triangle is
b = ½a = ½ × 4√3 = 2√3
The area of one small triangle is
A = ½ bh = ½× 2√3 × 6 = 6√3 in²
3. Calculate the area of the hexagon
A = 12 × 6√3 = 72√3 = 124.7 in²