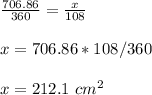Question

A scientist enlarged a circular portion of a microscope slide to make it easier to count the number of bacteria present in the sample.He divided the circle into 5 sectors as shown below and plans to count bacteria only in the shaded sector. What is the area of the shaded sector to the nearest tenth of a square centimeter

A.141.4
B.212.1
C.377.0
D.424.1

Answer 1

Option B.
`212.1\ cm^(2)`

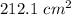
Explanation:

step 1

Find the central angle of the shaded sector

Remember that the diameter divide the circle into two equal parts ( 180 degrees each part)

so

Let

x -----> the measure of the central angle of the shaded sector

∠x+72°=180°

∠x=180°-72°=108°

step 2

Find the area of the circle

The area of the circle is

`A=\pi r^(2)`

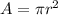
we have

`r=15\ cm`

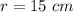
assume

`\pi=3.1416`

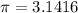
substitute

`A=(3.1416)(15)^(2)`

`A=706.86\ cm^(2)`

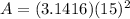
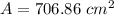
step 3

Find the area of the shaded sector

Remember that the area of the complete circle subtends a central angle of 360 degrees

so

by proportion find the area of a sector by a central angle of 108 degrees

`(706.86)/(360)=(x)/(108)\\ \\x=706.86*108/360\\ \\x=212.1\ cm^(2)`