Question

Determine the domain:


`f(x) = \frac{ln(ln(x + 1))}{e {}^(x) - 9 }`
​

Answer 1

The denominator cannot be zero, so

`e^x - 9 = 0 \implies e^x = 9 \implies x = \ln(9)`

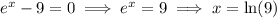
is not in the domain of
`f(x)`.

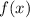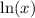`\ln(x)` is defined only for
`x>0`, and we have

`\ln(x+1) > 0 \implies e^(\ln(x+1)) > e^0 \implies x+1 > 1 \implies x>0`

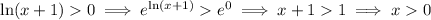
so there is no issue here.

By the same token, we need to have

`x+1 > 0 \implies x > -1`

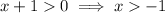
Taking all the exclusions together, we find the domain of
`f(x)` is the set

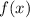`\left\{ x \in \Bbb R \mid x > 0 \text{ and } x \\eq \ln(9)\right\}`

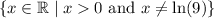
or equivalently, the interval
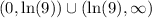`(0,\ln(9))\cup(\ln(9),\infty)`.